[10000印刷√] 立体 の 体積 ���題 203991-立体の体積 問題 難問

表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題
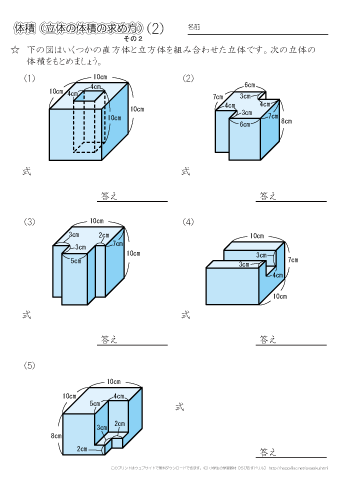
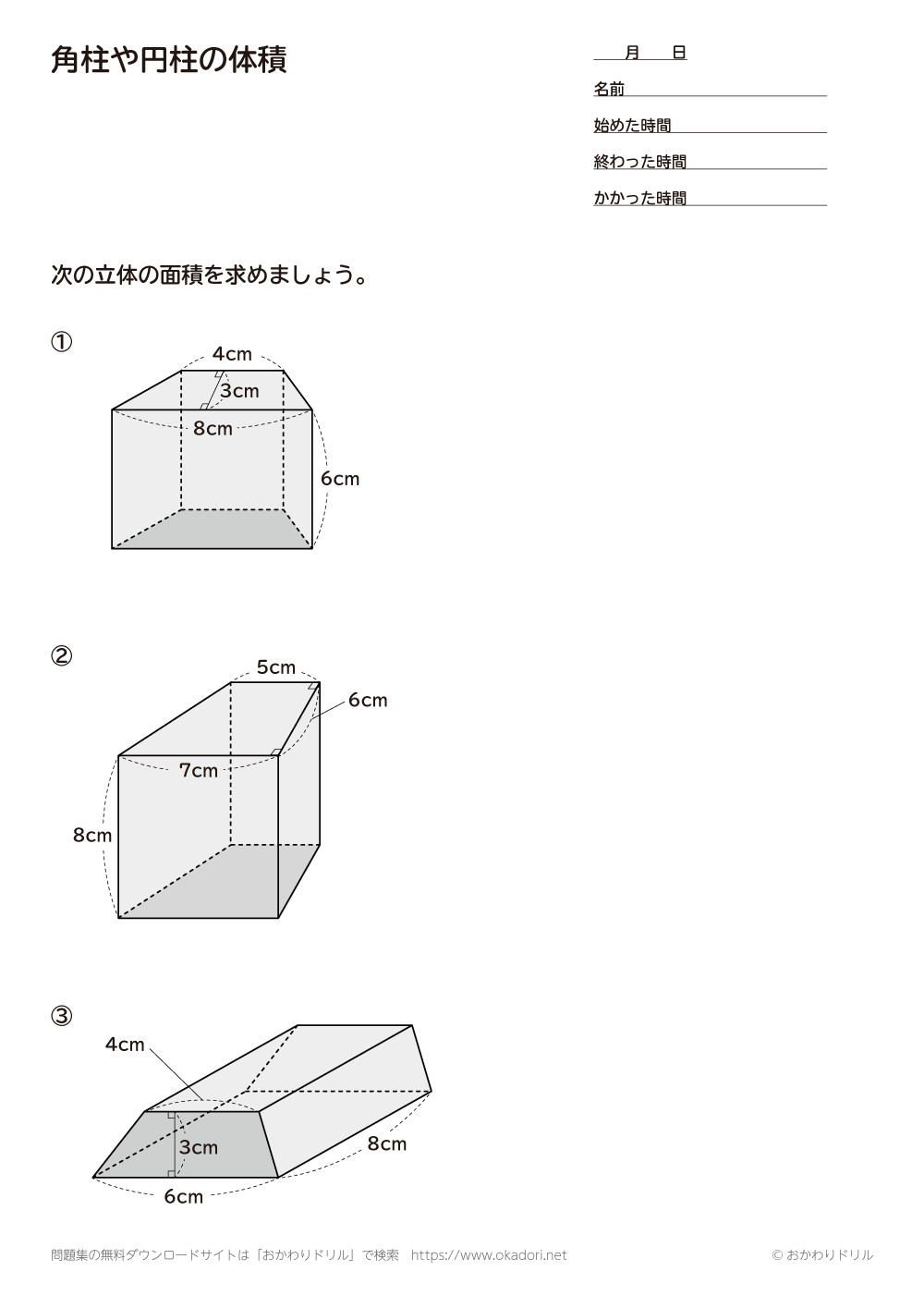
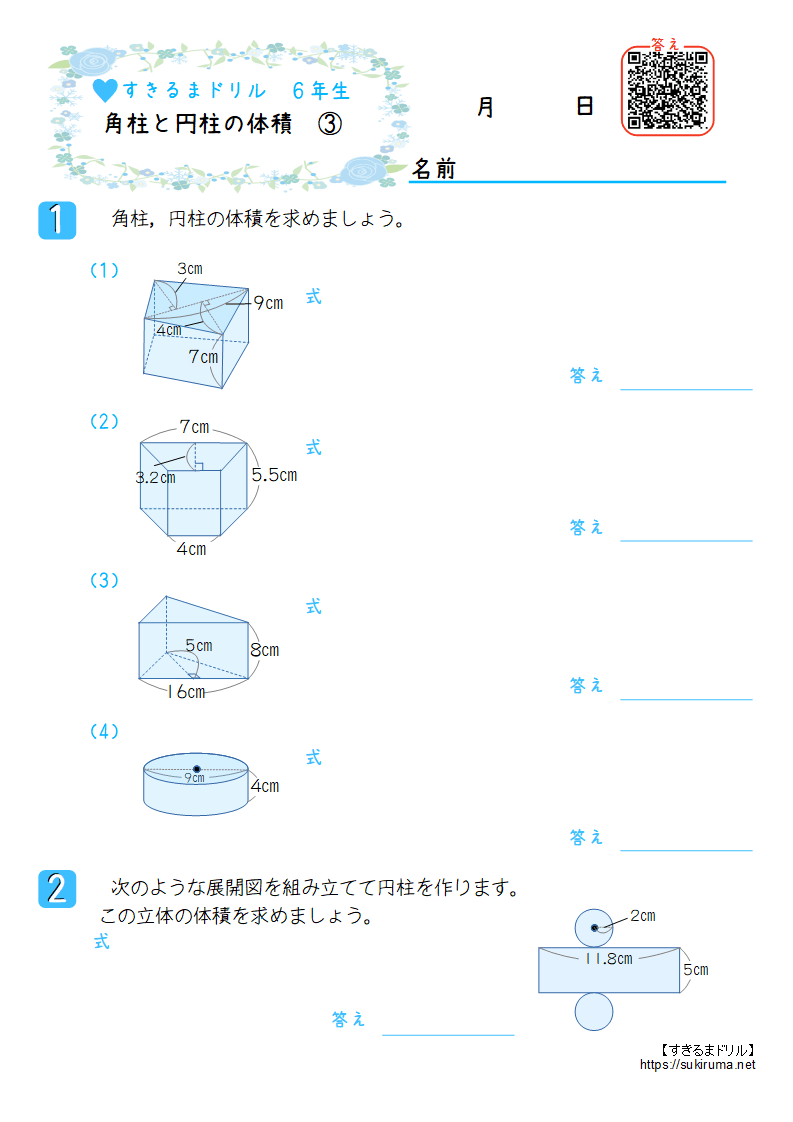
算数6年生「立体の体積(角柱・円柱)」のプリントです。 偶数番号のプリントは、奇数番号のプリントの内容で数値を変えただけとなっております。 この単元のプリント構成 1~2「立方体・直方体・三 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle
立体の体積 問題 難問
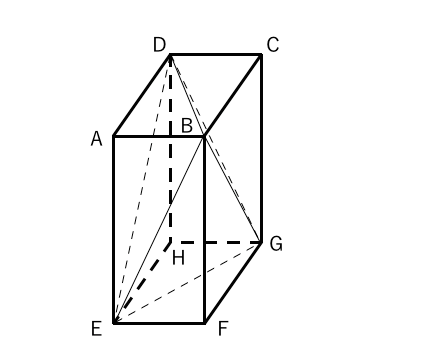
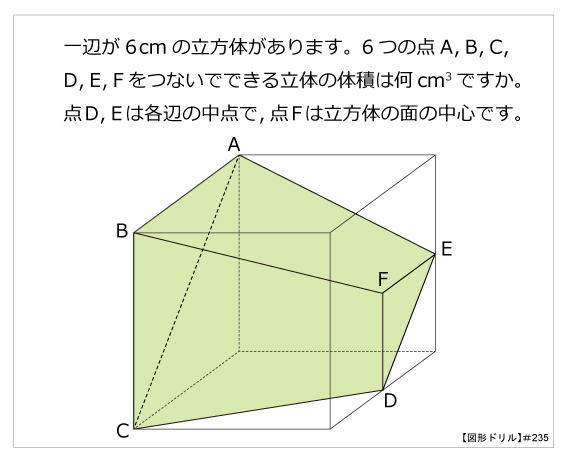
立体の体積 問題 難問-立方体・直方体 体積問題立方体・直方体 体積問題は、小学校5年生で習います基本の公式 直方体の体積=面積(縦×横)×高さ面積問題が分かればそれに高さを掛けるのが基本です単位に注意!面積の単位は㎠や㎡ですが、体積の場合は㎤や㎥になります。 問題例 下の図のような1辺6cmの立方体から3点a,c,fを通る平面で切り取ります。 作図をすると下のようになります。*作図のポイントは同じ平面上にある点を直線で結びます。 切り取った立体のうち点bをふくむ立体の体積を求めます。 底面積が三角形abc 高さがbfの三角すいの体積
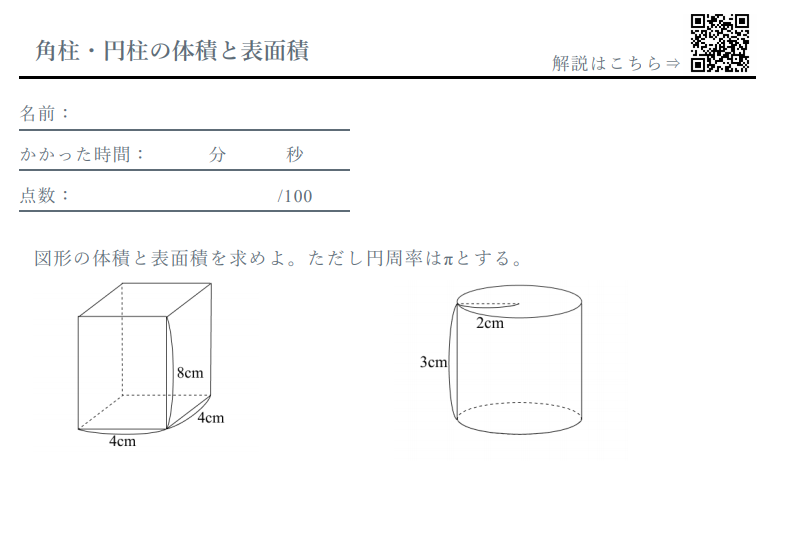
角柱 円柱の体積と表面積 計算ドリル 問題集 数学fun
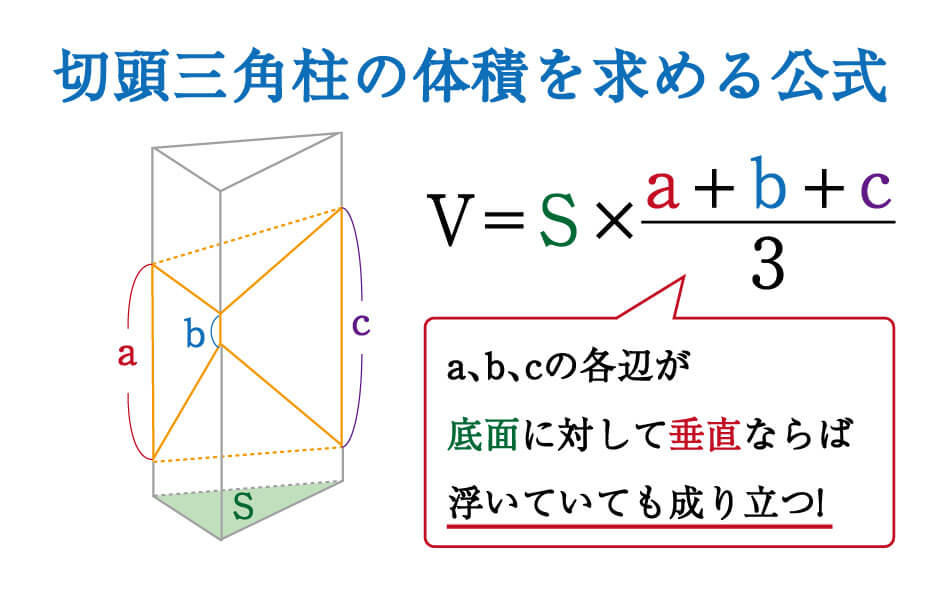
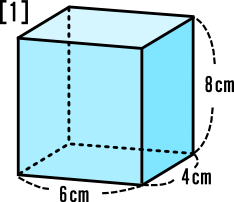
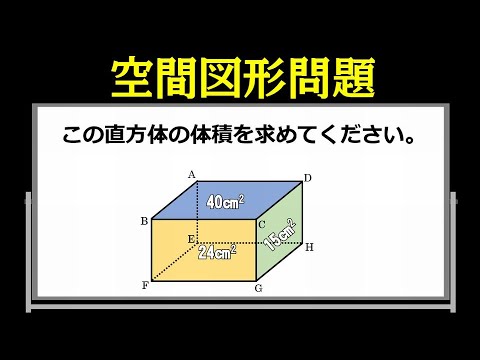
立体切断⑶ 体積 21 15 図のような1辺10㎝の立方体があり、点P、Q、Rは辺のまん中の点 です。この立方体を3点P、Q、Rを通る平面で切断し、2つの立体 に分けました。このとき、頂点Aを含む立体の体積を求めなさい。 右の図は直方体を斜めに切断したものです。 この立体の体積を求めてください。 入試では非常に有名な問題で、これは次のように解くというのが「常識」のようです。 36 × 11 6 4 9 4 = 270 つまり、「高さの平均」のようなものを考えて、それを底面積7 立体の体積と表面積 学基本学習の基本 37 切断と体積⑴ 問題 右の図は ,ab = 6 cmad ae 3 の直方体で ある。辺 ad の中点を m ,辺 bc の中点を n とし,この直方体を 次の平面で切るとき,頂点 a をふくむ方の立体の体積を求めよ。 ⑴ 3 点 m ,n,e を通る平面
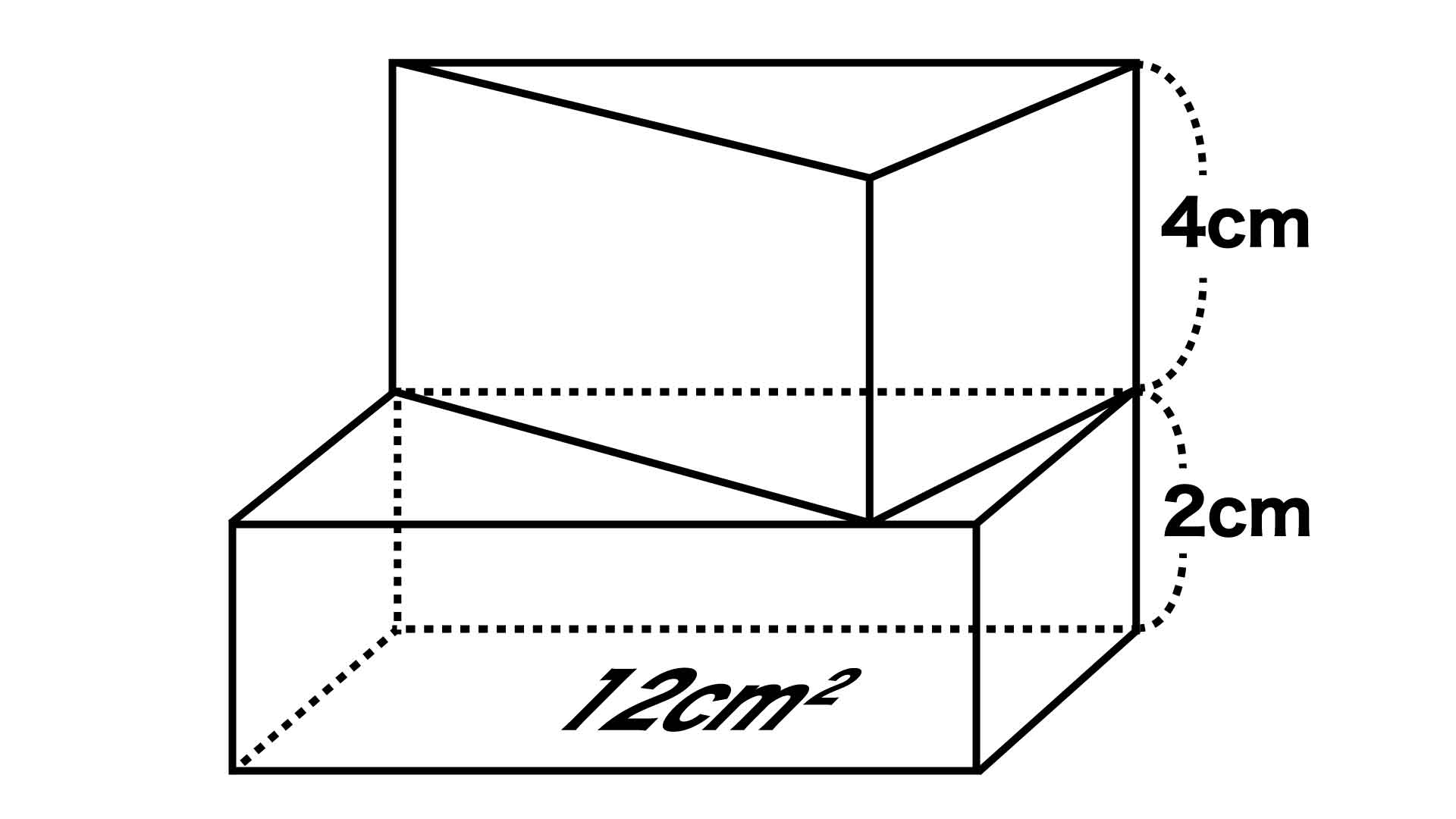
これら2つの直方体を足すと求める立体の体積になります。 \(2424=48\)となり、求める立体の体積は\(48cm^3\)となります。 まとめ 今回の記事では、直方体や立方体の体積を求める応用問題の考え方のコツについて、書いてみました。立体図形の総合問題(桜蔭中学 13年) 円すいを切った体積(大妻中学 13年) 長さ比と体積比は?(開成中学 過年度) 残った立体の体積は?(早稲田中学 14年) 表面積と体積は?(明星中学 10年) この立体図形の体積は?今回は立体図形のうち,回転体の問題に焦点をあて解説していきます。回転体の問題とは以下で紹介するような, 平面で提示された図形をある軸に沿って回転させ,そうしてできた立体の体積を求める ものです。 このような問題では平面上での図形の把握・空間上での図形の把握,という2
立体の体積 問題 難問のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 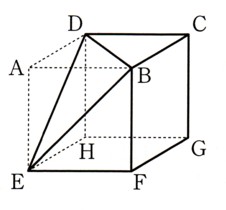 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
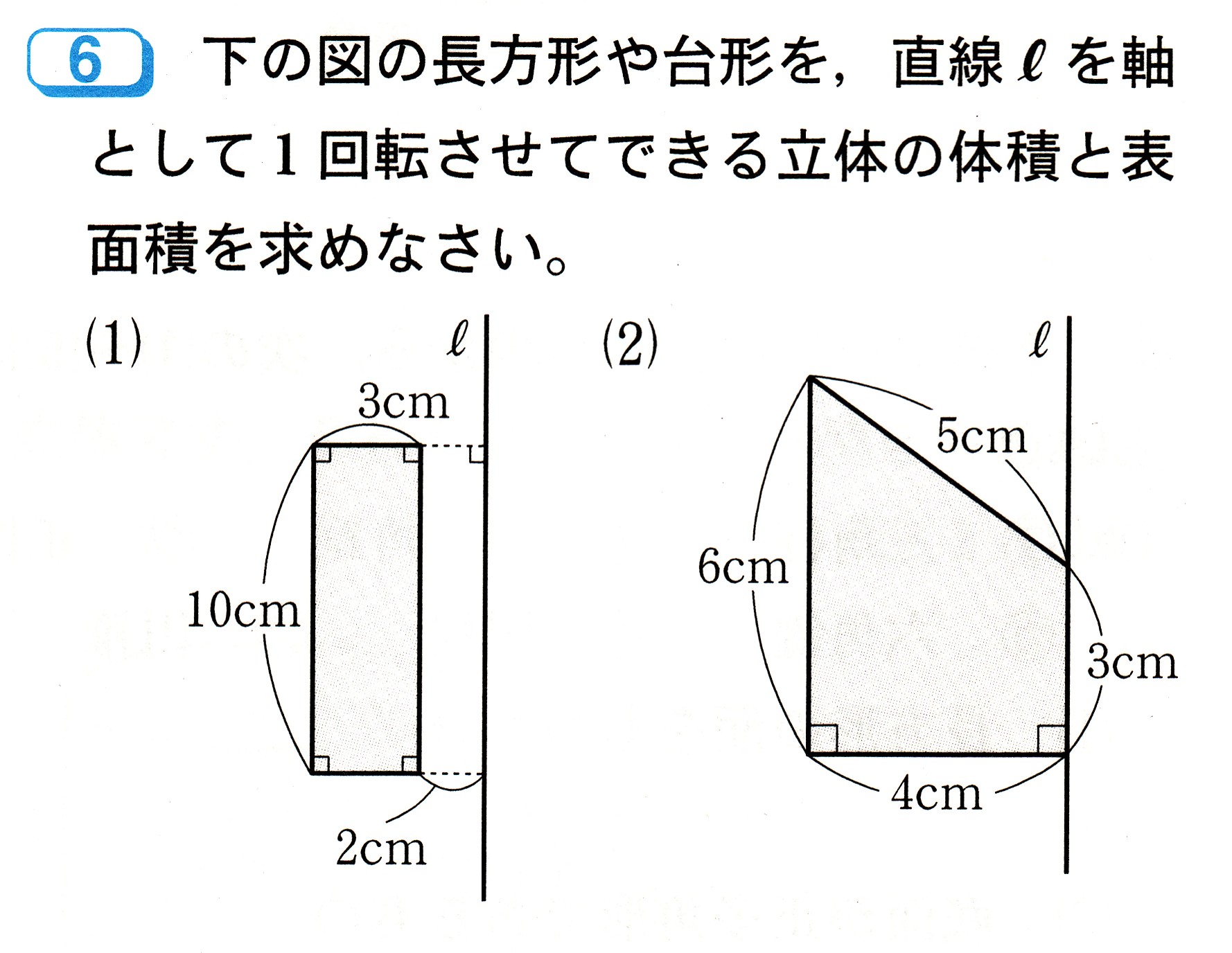 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 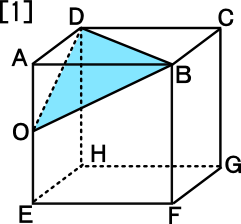 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 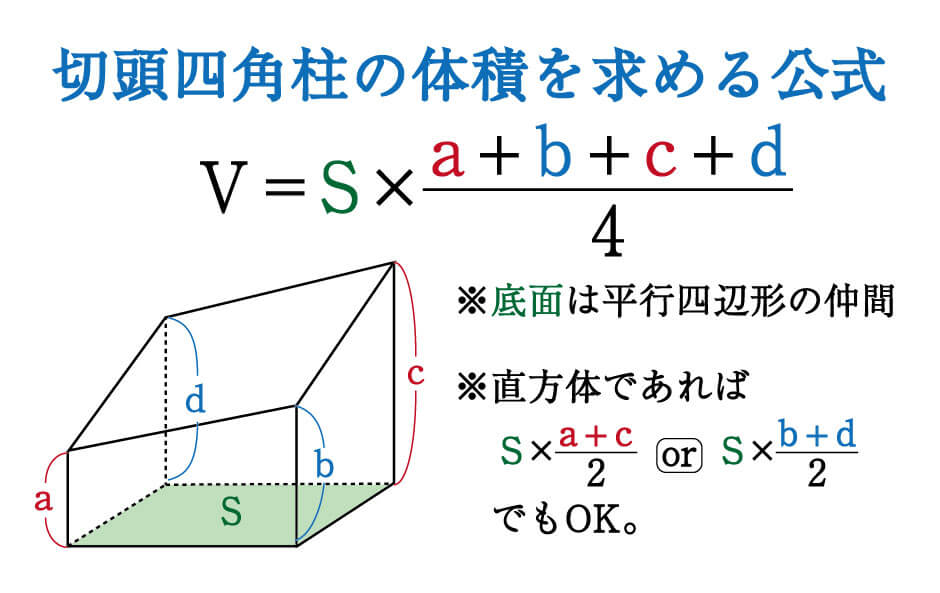 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 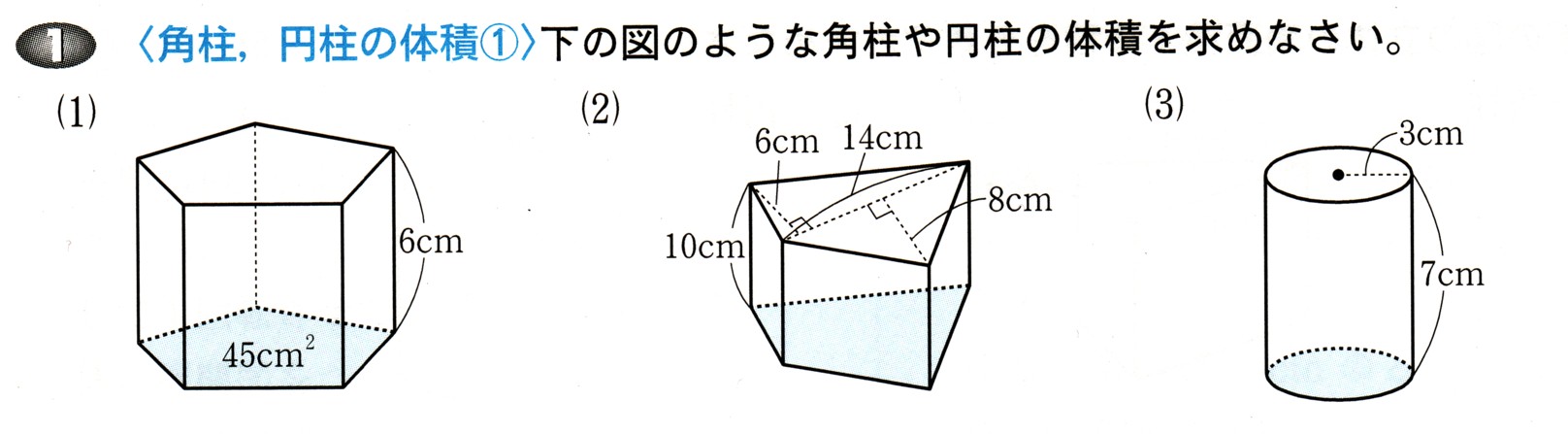 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 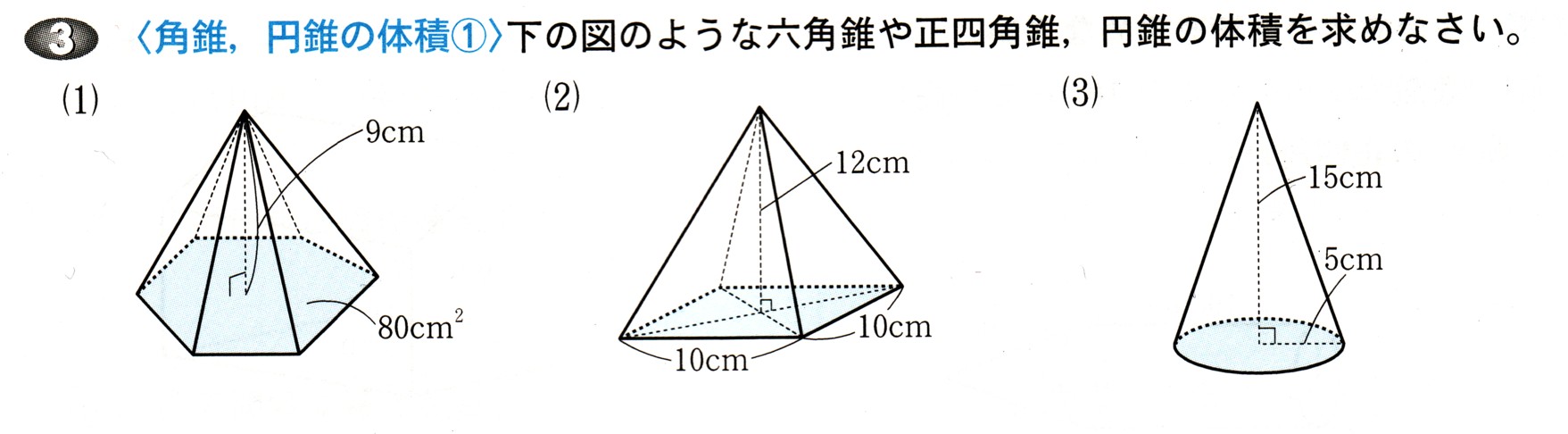 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 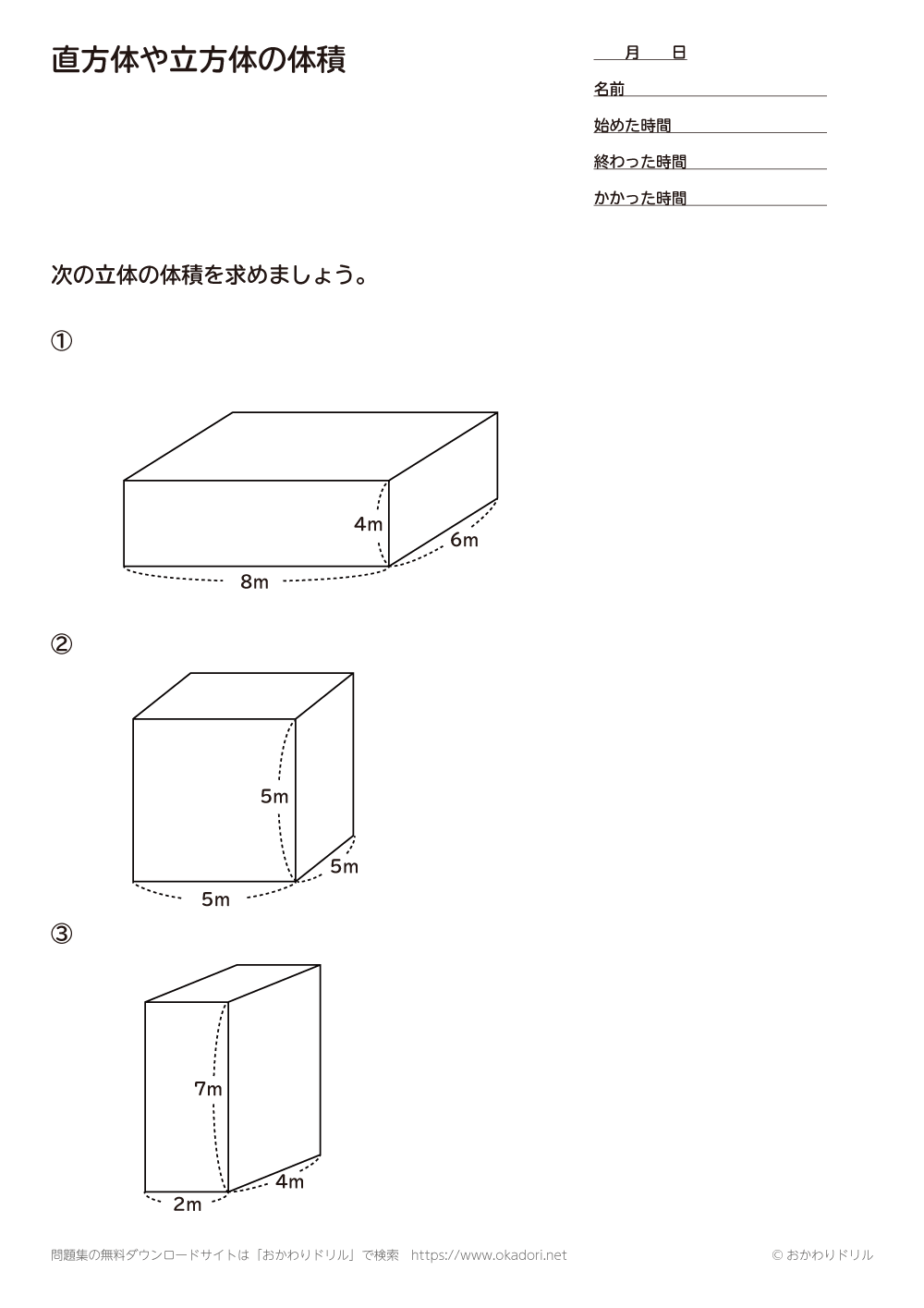 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 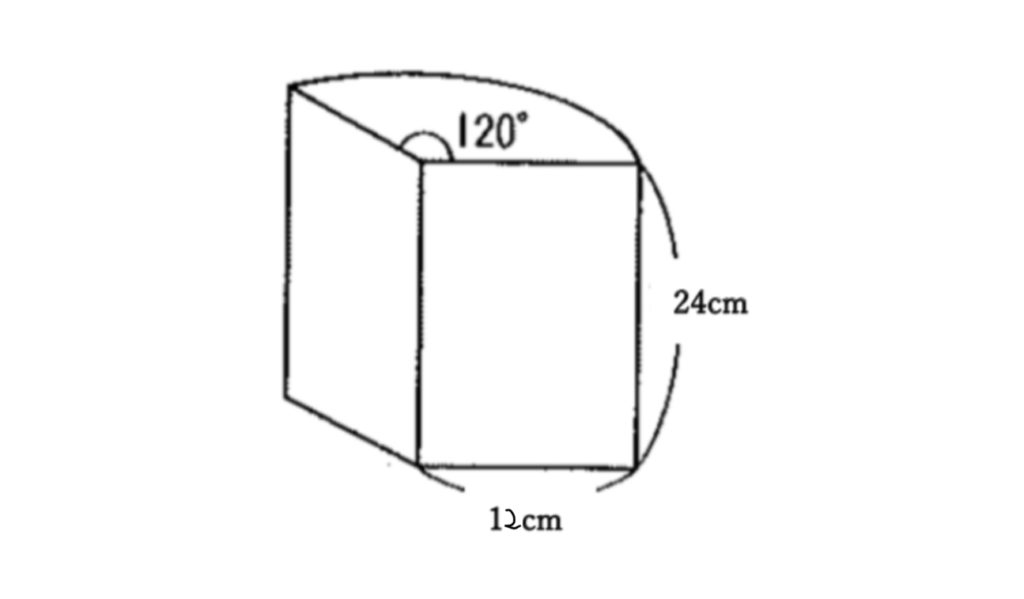 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 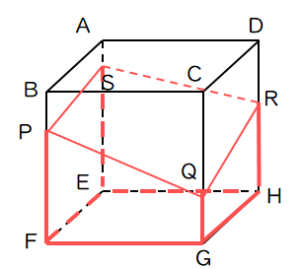 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 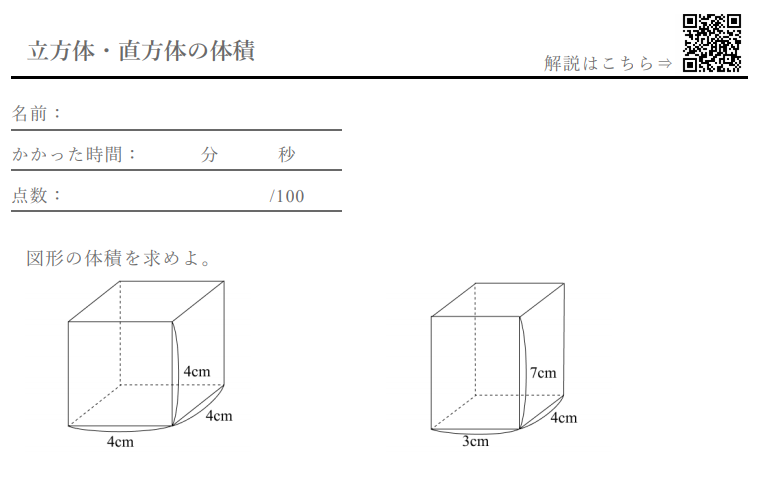 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 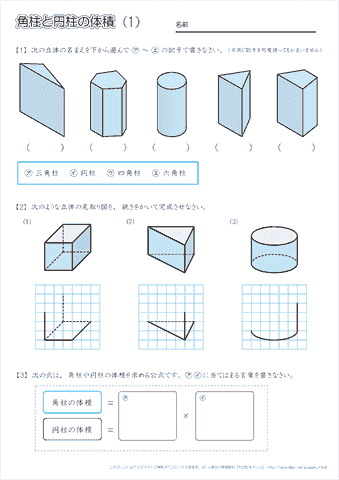 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 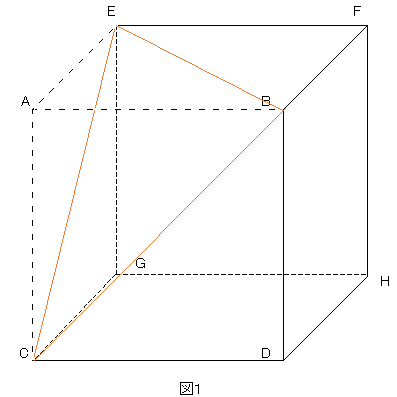 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 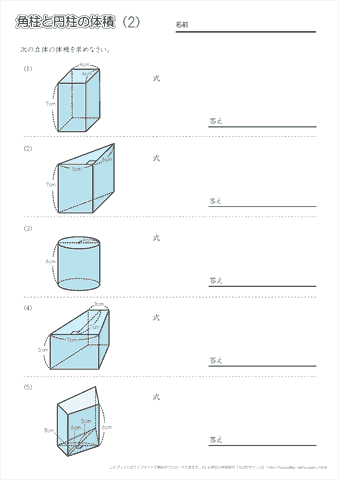 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 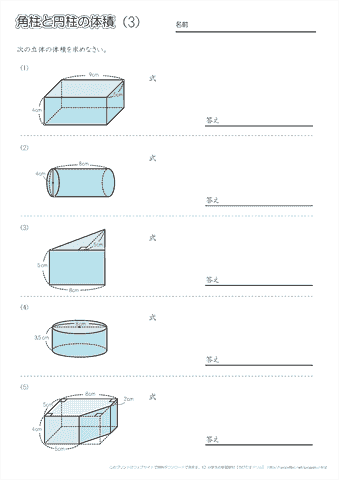 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 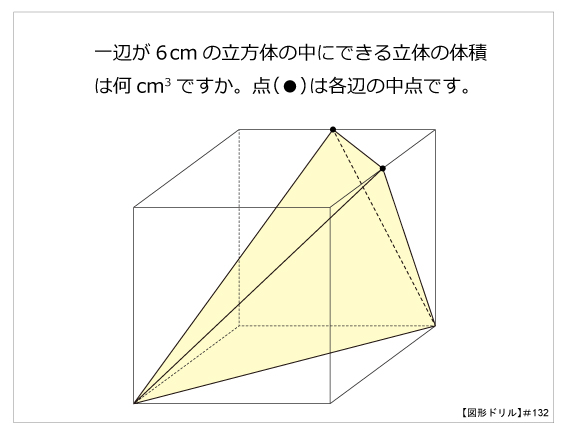 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 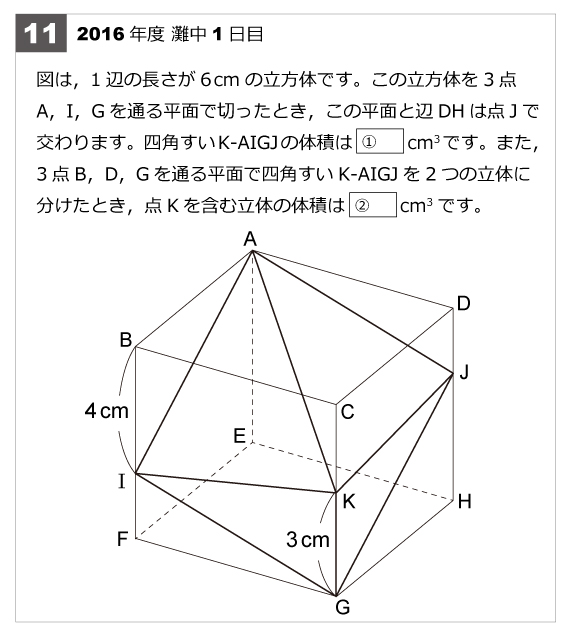 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 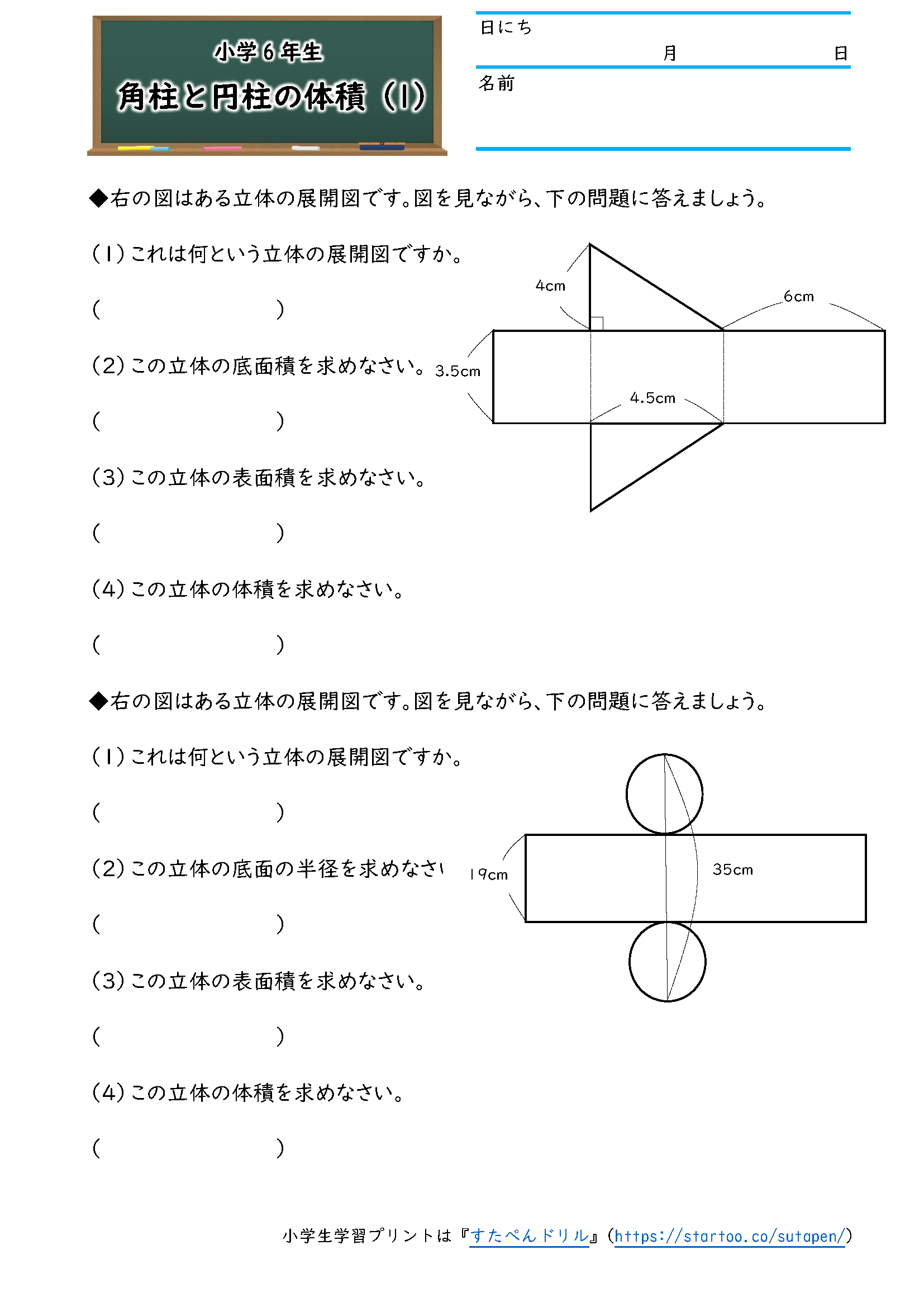 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 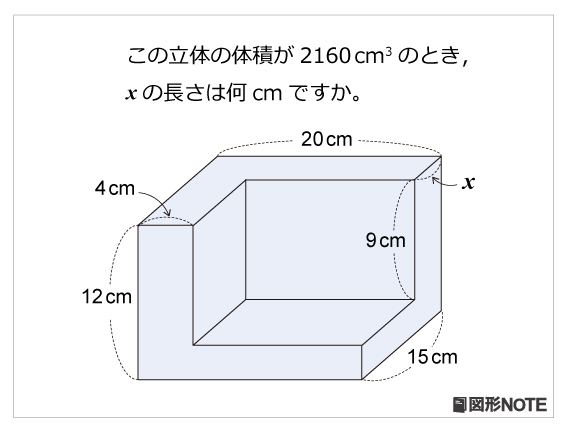 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 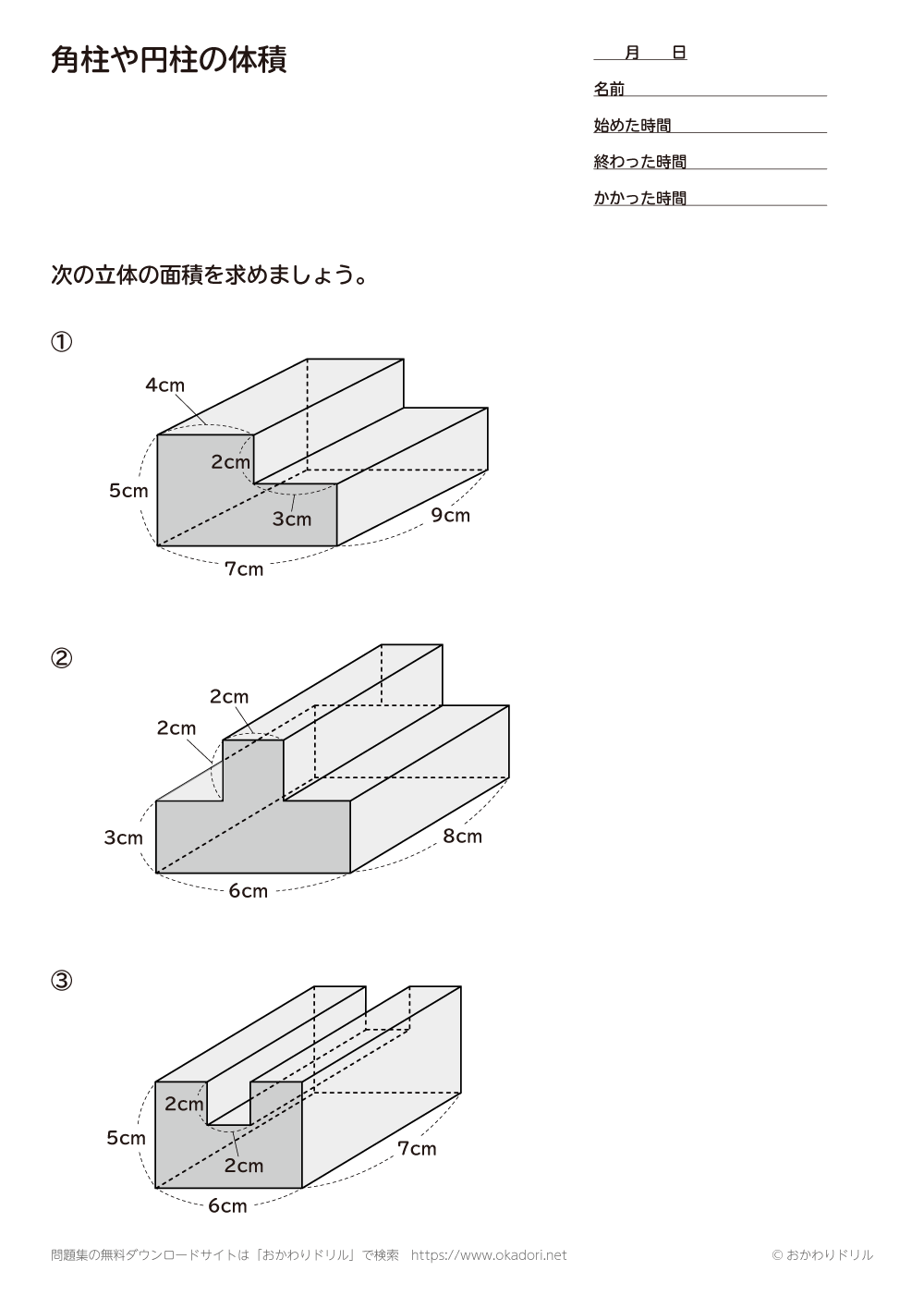 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 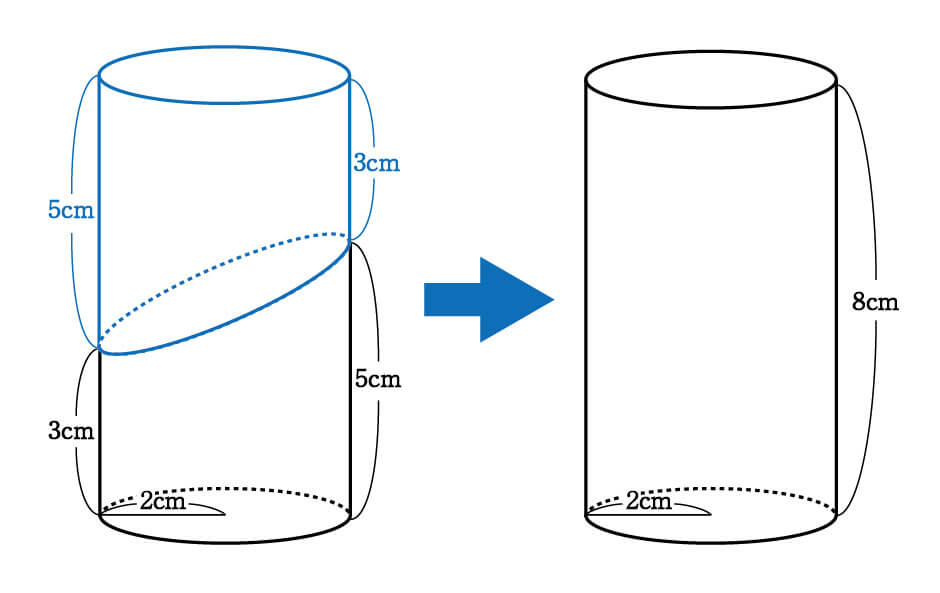 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 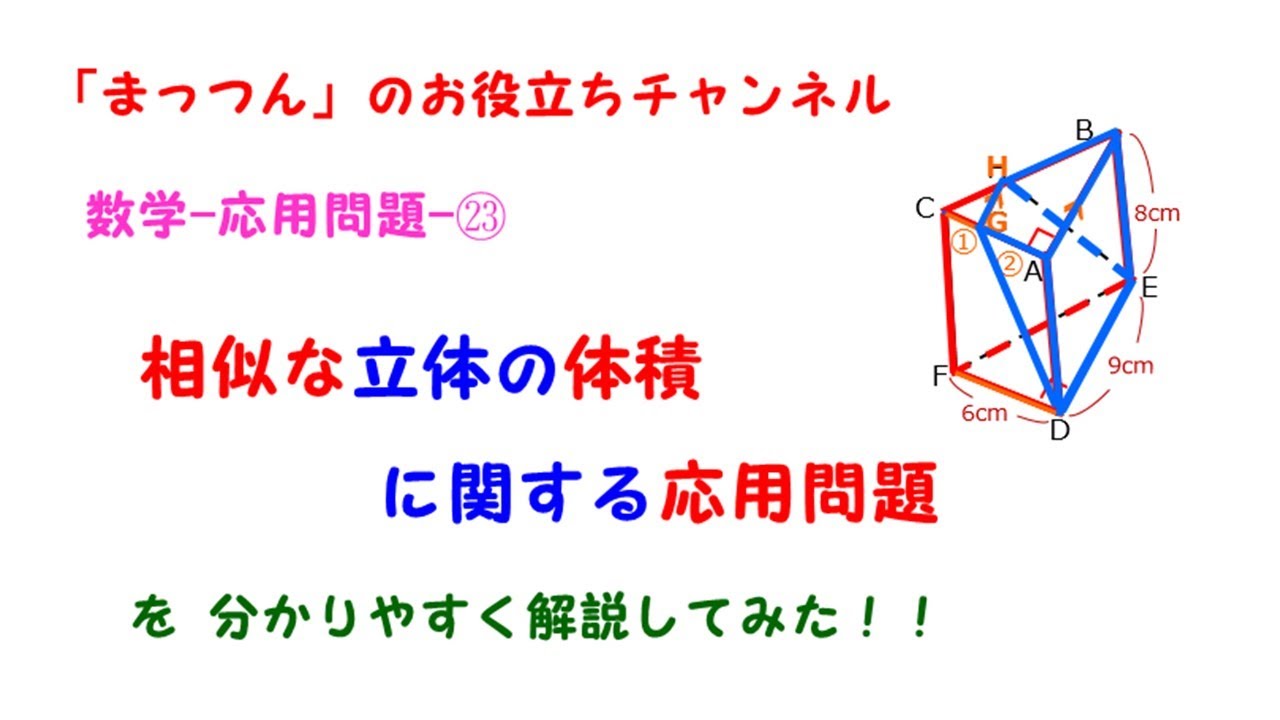 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 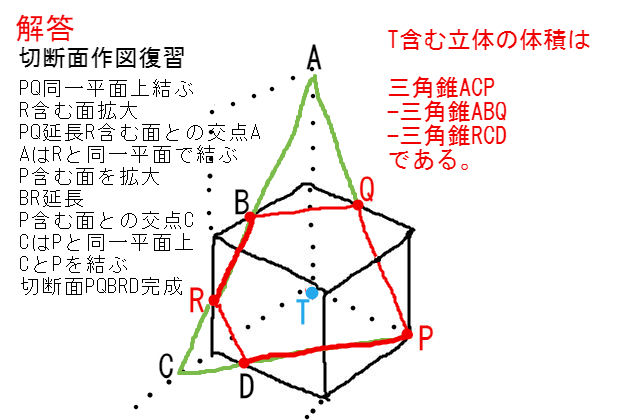 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 | 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
 北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |  北辰塾 情報局 直撃 中学入試問題 第166回 大妻 立体の体積 三角柱と回転体 |
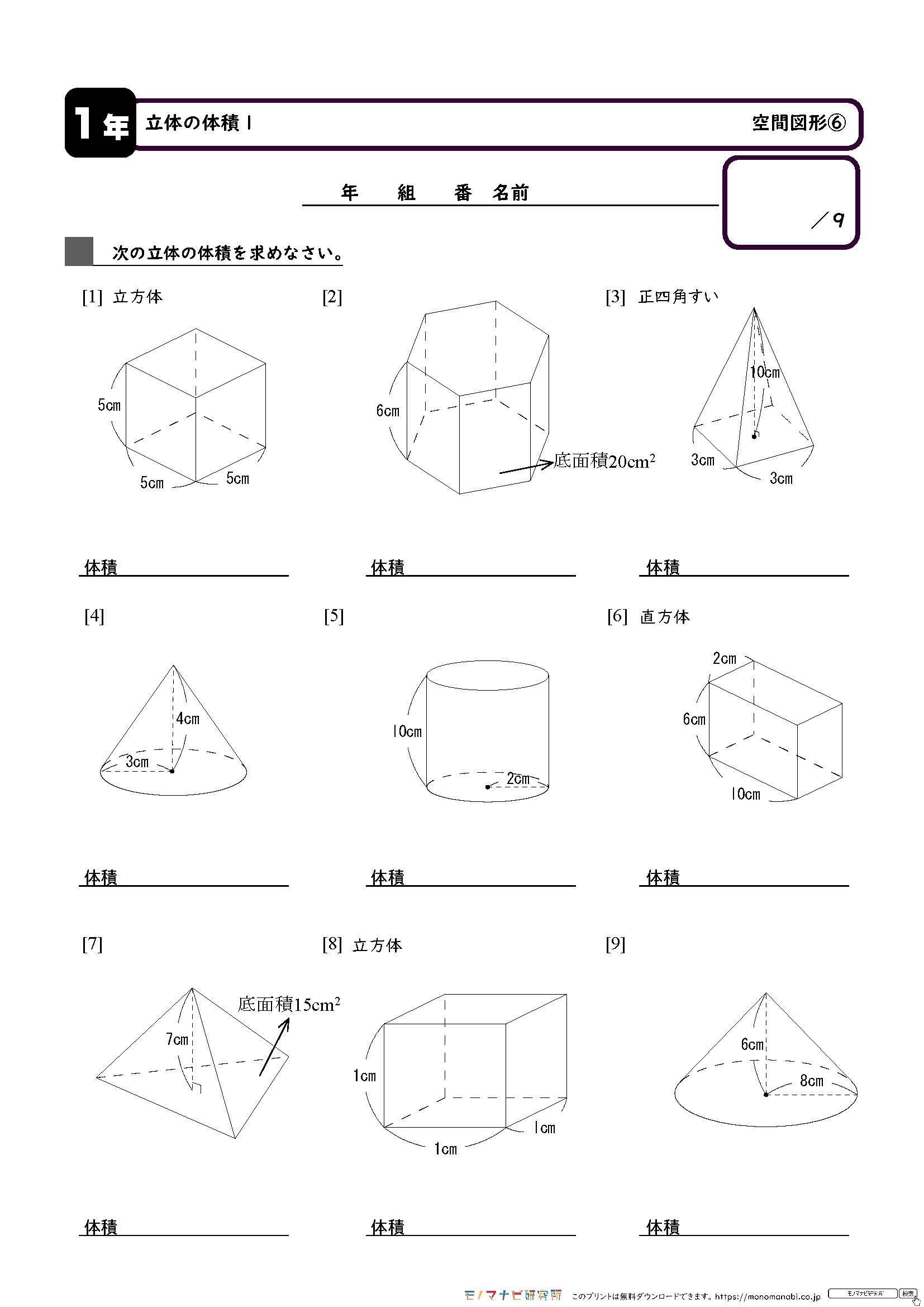
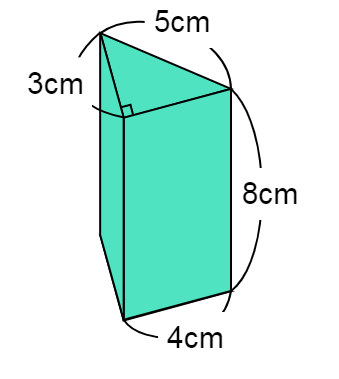
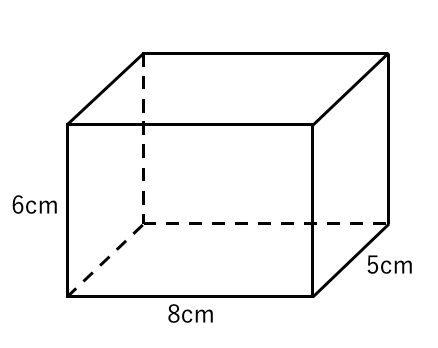
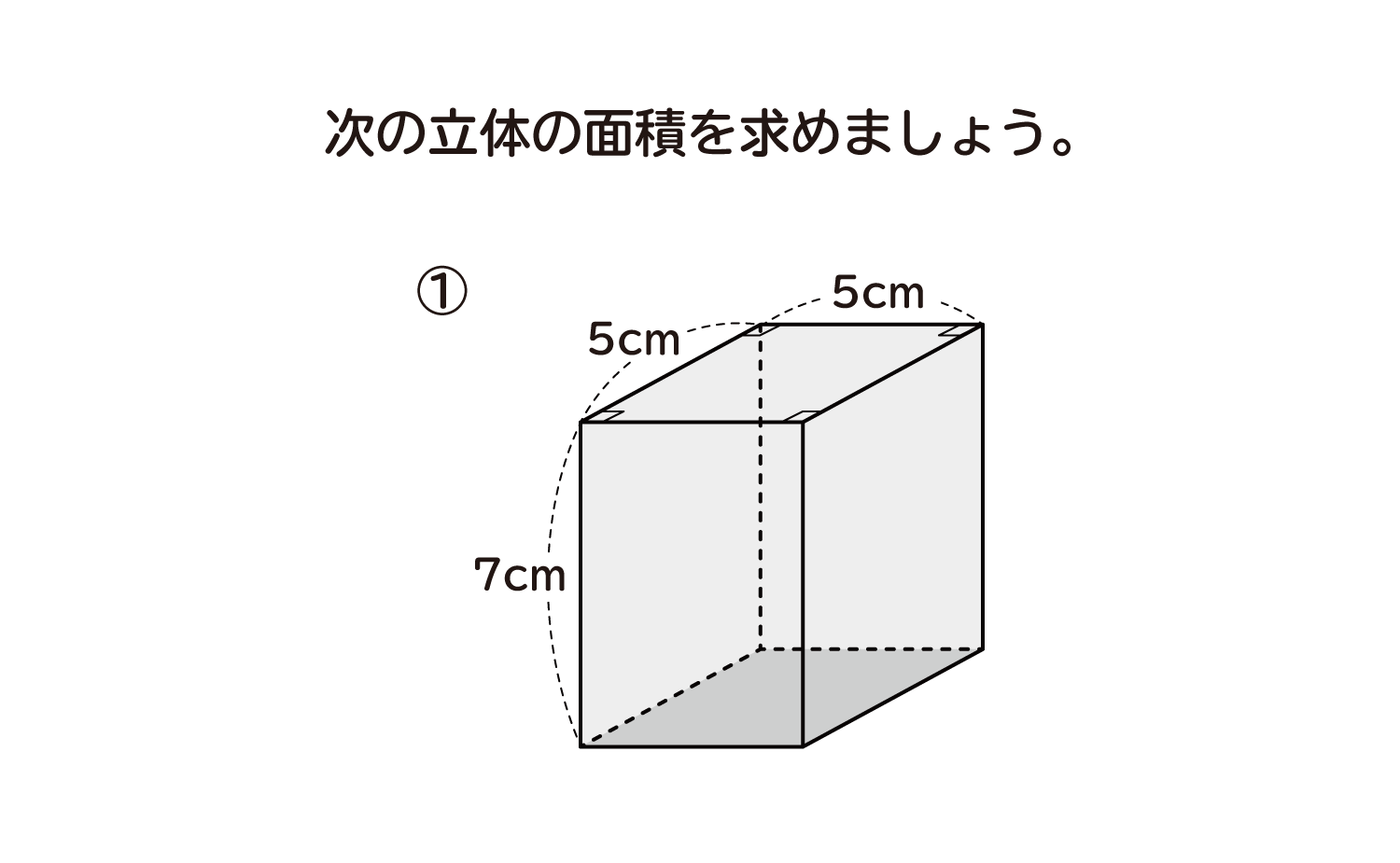
体積・表面積の練習問題 (1)下の図の三角柱で底面 ABCはAB=8cm,BC=6cm,AC=10cm,∠B=90°の直角三角形で、AD=9cmのとき、点A、D、E、Fを頂点とする三角錐AーDEFの体積を求めよ。 (2)図のように、1辺の長さが6cmの立方体がある。 4点A、C、F、Hを頂点とする立体の立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm
Incoming Term: 立体の体積 問題, 立体の体積 問題 中学, 立体の体積 問題 難問, 立体の体積 問題 6年生, 立体の体積 問題5年,
コメント
コメントを投稿